Light Motifs – Marcia Birken’s Images Meld Math and Art

Patterns are important to Marcia Katz Birken ’71. As a mathematics professor at Rochester Institute of Technology (RIT) for nearly three decades, Birken taught about the elegant patterns numbers make. But a nature tour of Yellowstone National Park in 2005 sent her love of patterns in a new direction. “I was looking at the same things everyone else was, but I saw different things. They’d see flowers; I’d see rotational patterns in the petals. They’d see a landscape; I’d see patterns repeated in the meanders of the river. They’d see birds; I’d see how the feathers grew.” (Birken Photo: Leichtner Studios)
That moment of revelation brought together her love of the natural world and the mathematical world. Now retired from RIT, she pursues these merged interests through a third one, photography. Joined by husband Eric, Birken and her trusty Canon digital have camped across Botswana, explored Chilean Patagonia, and sailed to Antarctica on the icebreaker The Endeavor.


Wherever the site and whatever the sights, Birken finds patterns—“from the regular striping of zebras to the random scattering of wildflowers in a meadow; from mountains reflected exactly in calm waters to mangrove roots mirrored with distortion in swampy ripples; from the regular patterns of symmetry to the rough and jagged patterns of fractals; from number series in math to a series of birds in flight.”
Peering through a camera, Birken saw fractal patterns in Antarctic icebergs. She found Fibonacci sequences (a specific kind of repeating pattern) in the spirals formed by bracts of pinecones and the central disks of composite flowers, such as daisies. “I found patterns in nature that I had been describing mathematically,” she recalls. This realization bloomed into a new book, cowritten with professor/poet Anne C. Coon. Discovering Patterns in Mathematics and Poetry uses Birken’s nature photos to illustrate mathematical concepts, such as the Golden Mean, logarithmic spirals, and four types of symmetry.
Combining the scientific and the artistic isn’t new to Birken. “My whole career life has been based on what I learned at MHC. I majored in math and minored in religion. That [combination] seemed completely logical because I was educated to see everything in the world as connected.”
She and Eric (a physician with a flexible schedule) decide “quite spontaneously” when and where to travel, mostly joining small nature-travel groups. Their adventures have already included South Africa, Ecuador, Iceland, Israel, Britain, China, Costa Rica, and most recently, New Zealand. Visits to Yosemite and Glacier National Parks are on the horizon.
Although Birken’s photos are sold on her Web site and at occasional shows near her home, she says she’s “having too much fun [traveling] to organize the business end. Our kids are settled, so it’s easy to pick up and go. And I want to go everywhere!”
Learn More
 This Web-exclusive content is offered in connection with the fall 2008 Mount Holyoke Alumnae Quarterly magazine article “Light Motifs: Marcia Birken’s Images Meld Math and Art” by Emily Harrison Weir.
This Web-exclusive content is offered in connection with the fall 2008 Mount Holyoke Alumnae Quarterly magazine article “Light Motifs: Marcia Birken’s Images Meld Math and Art” by Emily Harrison Weir.
Photos and explanations by Marcia Katz Birken ’71
FIBONACCI NUMBERS & GOLDEN SPIRALS
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, . . .
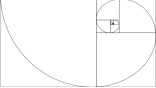
This list of numbers is the famous Fibonacci Sequence (or Fibonacci Numbers), named after the 12th century Italian mathematician, Leonardo of Pisa, known colloquially as Fibonacci or “son of Bonacci.” After the first two 1’s, each number is the sum of the two previous numbers (2 = 1 + 1; 3 = 1 + 2; 5 = 2 + 3; etc.). Fibonacci Numbers are intriguing, not only because of their mathematical pattern, but also because this particular sequence is closely linked to growth in nature. The pattern in which leaves occur on a stem, the number of petals or petal-like parts on some wildflowers, and the arrangement in the packing of seeds are all closely linked to Fibonacci Numbers. The daisy is an example of a composite flower, made up of disc florets in the center and ray florets (or petals) on the outside. The disc florets are arranged in clockwise and counterclockwise spirals. The numbers of spirals in each direction are consecutive Fibonacci Numbers. This relationship is echoed in spirals found in pinecones, pineapples, ginger plants, artichokes, and other plants. The spirals themselves are Golden Spirals, based on the Golden Ratio, whose exact value is approximately [1.61803. . .]. The ratio can be found by taking the limit of consecutive Fibonacci Numbers. This is the spiral of equiangular growth and is also displayed in the nautilus and other shells, in the seeds of sunflowers, and the horns of many animals.
This daisy, from Adirondack State Park, NY, was shot and cropped to emphasize the spirals appearing in the central disc florets. On the second and third photos, I have traced out the 21 clockwise and 34 counterclockwise spirals. 21 and 34 are consecutive Fibonacci Numbers. The spirals are Golden Spirals. There is also rotational symmetry in the petals or ray florets of the daisy (see SYMMETRY below).
The bracts of the red ginger plant from Costa Rica are also arranged in two sets of Golden Spirals. The numbers of clockwise and counterclockwise spirals are consecutive Fibonacci Numbers.

The unfurled spiral of this fiddlehead fern from Costa Rica is not a Golden Spiral. When tightly wound, it resembles an Archimedes’ Spiral and as it unfurls it looks more like a Hyperbolic Spiral.
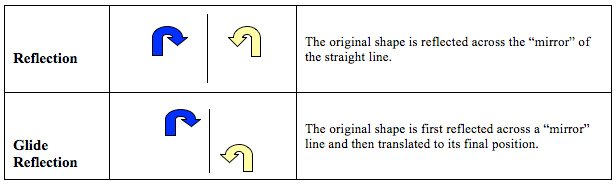
SYMMETRY
Mathematicians define four types of symmetry, as shown in this table:
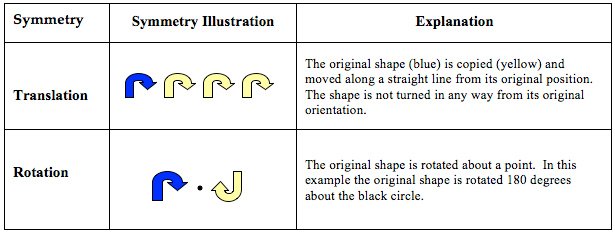
Symmetry in nature may occur in natural growth patterns, such as the reflection pattern of butterfly wings, translation pattern of leaves, or rotation pattern of flower petals. Symmetry may also be found serendipitously in fleeting moments of birds in flight or through camera angles that show translation or reflection.
This Antarctic landscape shows exact reflection symmetry in a rare moment of still ocean waters.

A mangrove swamp in the Galapagos Islands shows distorted reflection symmetry as our slow-moving boat creates gentle ripples in the water.
Scarlet macaws fly in formation at dusk just outside the Carara Biological Reserve in Costa Rica. Their heads, body positions, and tails mimic translation symmetry, while their wings mimic reflection symmetry.

Black-faced ibis fly over Laguna Nimez Wildlife Sanctuary in Patagonian Argentina. Their heads and bodies mimic translation symmetry, while their wings mimic reflection symmetry.
When shot from a certain angle, this s
tand of large tree ferns in Costa Rica shows reflection symmetry.
Each branch of the fish tail palm of Costa Rica exhibits translation and glide translation symmetries, while corresponding leaves exhibit reflection symmetry.
This grove of aspens in Snowmass, Colorado, shows translation and glide translation symmetries from this camera angle.
Many mathematical concepts appear in this shot of fritillary butterflies on a composite flower in Adirondack State Park, NY. The butterflies’ wings exhibit exact reflection symmetry of their intricate pattern, while the petals of the coneflower exhibit rotational symmetry. The disc florets of the flower form two sets of Golden Spirals. The numbers of spirals in each set are consecutive Fibonacci Numbers.
SPOTS AND STRIPES
How did the leopard, cheetah, or giraffe get their spots? Why do the tiger and zebra have stripes instead of spots? It is all part of the complicated topic of morphogenesis—an aspect of developmental biology dealing with the formation of an organism and its parts. Mathematicians have proposed models of spot/stripe patterning based on the work in the 1950’s by the British mathematician, Alan Turing. Turing showed that while diffusion is usually a process that creates more uniformity, it may also destabilize a chemical system and produce patterning instead. Turing’s Reaction-Diffusion Equations have been used to develop models of different skin patterning caused by the diffusion of chemicals and their reactions in embryonic cells.
This cropping of two Burchell’s zebras feeding in the Okavango Delta of Botswana emphasizes their striping pattern—a pattern unique in every animal.
Similarly, the spotted pattern of a cheetah found in the Savuti Region of Botswana stands out in this close-up photo. Also noticeable are the rings at the end of the tail where the spots have morphed into stripes.

FRACTALS
A fractal image is one in which instances of either the entire work, or selected pieces of the work, are repeated. Perhaps each repetition is an exact replica of the original piece, or, more likely, the repetition just approximates the original. For instance, a single frond of a fern is a miniature version of the entire plant, much like a single floweret of broccoli resembles the entire head. From a mathematical point of view:
A fractal is a mathematical object, such as a curve, that displays exact or approximate self-similarity on different scales. The image of a fractal is frequently obtained from a recursive or iterative formula and when magnified, the resulting detail looks surprisingly similar to the original object.
One fractal, the Koch Snowflake, is constructed by iteratively removing one third of each side of an equilateral triangle. The portion that is removed is replaced by another equilateral triangle whose side is 1/3 the length of the previous iteration.
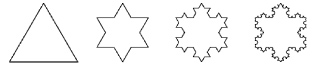
Many images in nature exhibit qualities similar to mathematical fractals.
The rocks on a beach in Olympic National Park, Washington, form a fractal-like pattern. If we zoomed in on a small part of the rocky beach it would resemble the entire beach.
Each part of the dandelion head, photographed in Iceland, resembles the entire head.
Zooming in on any portion of this Antarctic iceberg would produce a pattern similar to the overall pattern of the iceberg. Also the “fractured” outer edge of the berg has the jagged pattern similar to the fractal edge of a famous Koch Snowflake.
This close-up of another Antarctic iceberg shows the bubbles forming a fractal-like pattern.
Minerva Terrace, an extinct geyser in Yellowstone National Park, appears fractal-like in the white travertine steps and layers formed by mineral run-off. The same step-like pattern can be seen in the cyanobacteria mat formed from runoff of an active geyser in Yellowstone.
November 27, 2008


















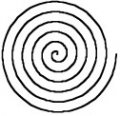
 Koch Snowflake
Koch Snowflake








I made an interesting discovery not to long ago which incorporates the golden ratio, the Mayan calendar and a major time of influence in our world.
In the Mayan calendar, an enoch is 1,869,530 days. The beginning of the last enoch is calculated to be between August 11th and September 6th 3114 BCE. The last day of this enoch is calculated to be December 12, 2012. In the mayan tradition this is supposed to represent an epic change or rebirth of things.
I was initially curious about what date landed in the middle of these to dates (the mid-life of this cycle). It didn’t prove anything interesting. However, for some strange reason I decided to calculate the golden ratios of this amount of days (1,869,530) to see what was going on around this time of the world. What I found was that the end of the first segment (shorter segment) of the ratio came around 52 AD. I am not a mathematician so my calculation may be off just a tad. However, that would put the golden ratio very near the time of Jesus. Hope it gives you something interesting to think about.
Thank you Mt. Holyoke Quarterly for the Birken article and web address. This is fascinating and I look forward to broadening my appreciation of nature and learning more about the mathematical concepts connected with it. Hooray for the Internet and Mt. Holyoke.
I am grateful to GOOGLE for drawing me to this article and even more grateful to Marcia for her good eye and the lovely images. Thank you.